

Nuclear Magnetic Resonance spectroscopy is a powerful and theoretically complex analytical tool. On this page, we will cover the basic theory behind the technique. It is important to remember that, with NMR, we are performing experiments on the nuclei of atoms, not the electrons. The chemical environment of specific nuclei is deduced from information obtained about the nuclei.
Subatomic particles (electrons, protons and neutrons) can be imagined as spinning on their axes. In many atoms (such as 12C) these spins are paired against each other, such that the nucleus of the atom has no overall spin. However, in some atoms (such as 1H and 13C) the nucleus does possess an overall spin. The rules for determining the net spin of a nucleus are as follows;
The overall spin, I, is important. Quantum mechanics tells us that a nucleus of spin I will have 2I + 1 possible orientations. A nucleus with spin 1/2 will have 2 possible orientations. In the absence of an external magnetic field, these orientations are of equal energy. If a magnetic field is applied, then the energy levels split. Each level is given a magnetic quantum number, m.
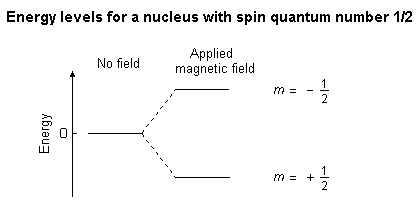
When the nucleus is in a magnetic field, the initial populations of the energy levels are determined by thermodynamics, as described by the Boltzmann distribution. This is very important, and it means that the lower energy level will contain slightly more nuclei than the higher level. It is possible to excite these nuclei into the higher level with electromagnetic radiation. The frequency of radiation needed is determined by the difference in energy between the energy levels.
The nucleus has a positive charge and is spinning. This generates a small magnetic field. The nucleus therefore possesses a magnetic moment, m, which is proportional to its spin,I.
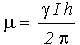
The constant, g, is called the magnetogyric ratioand is a fundamental nuclear constant which has a different value for every nucleus. h is Plancks constant.
The energy of a particular energy level is given by;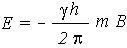
Where B is the strength of the magnetic field at the nucleus.
The difference in energy between levels (the transition energy) can be found from
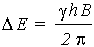
This means that if the magnetic field, B, is increased, so is DE. It also means that if a nucleus has a relatively large magnetogyric ratio, then DE is correspondingly large.
If you had trouble understanding this section, try reading the next bit (The absorption of radiation by a nucleus in a magnetic field) and then come back.
In this discussion, we will be taking a "classical" view of the behaviour of the nucleus - that is, the behaviour of a charged particle in a magnetic field.
Imagine a nucleus (of spin 1/2) in a magnetic field. This nucleus is in the lower energy level (i.e. its magnetic moment does not oppose the applied field). The nucleus is spinning on its axis. In the presence of a magnetic field, this axis of rotation will precess around the magnetic field;
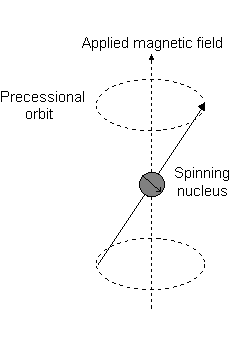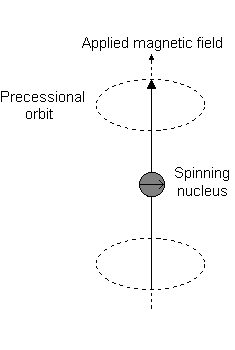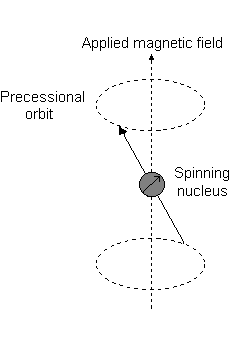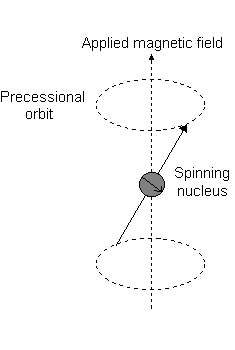
The frequency of precession is termed the Larmor frequency, which is identical to the transition frequency.
The potential energy of the precessing nucleus is given by;
E = - m B cos q
where q is the angle between the direction of the applied field and the axis of nuclear rotation.
If energy is absorbed by the nucleus, then the angle of precession, q, will change. For a nucleus of spin 1/2, absorption of radiation "flips" the magnetic moment so that it opposes the applied field (the higher energy state).
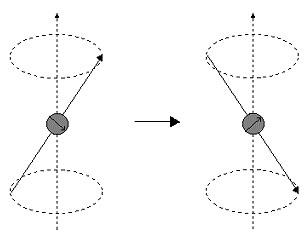
It is important to realise that only a small proportion of "target" nuclei are in the lower energy state (and can absorb radiation). There is the possibility that by exciting these nuclei, the populations of the higher and lower energy levels will become equal. If this occurs, then there will be no further absorption of radiation. The spin system is saturated. The possibility of saturation means that we must be aware of the relaxation processes which return nuclei to the lower energy state.
How do nuclei in the higher energy state return to the lower state? Emission of radiation is insignificant because the probability of re-emission of photons varies with the cube of the frequency. At radio frequencies, re-emission is negligible. We must focus on non-radiative relaxation processes (thermodynamics!).
Ideally, the NMR spectroscopist would like relaxation rates to be fast - but not too fast. If the relaxation rate is fast, then saturation is reduced. If the relaxation rate is too fast, line-broadening in the resultant NMR spectrum is observed.
There are two major relaxation processes;
Spin - lattice relaxation
Nuclei in an NMR experiment are in a sample. The sample in which the nuclei are held is called the lattice. Nuclei in the lattice are in vibrational and rotational motion, which creates a complex magnetic field. The magnetic field caused by motion of nuclei within the lattice is called the lattice field. This lattice field has many components. Some of these components will be equal in frequency and phase to the Larmor frequency of the nuclei of interest. These components of the lattice field can interact with nuclei in the higher energy state, and cause them to lose energy (returning to the lower state). The energy that a nucleus loses increases the amount of vibration and rotation within the lattice (resulting in a tiny rise in the temperature of the sample).
The relaxation time, T1 (the average lifetime of nuclei in the higher energy state) is dependant on the magnetogyric ratio of the nucleus and the mobility of the lattice. As mobility increases, the vibrational and rotational frequencies increase, making it more likely for a component of the lattice field to be able to interact with excited nuclei. However, at extremely high mobilities, the probability of a component of the lattice field being able to interact with excited nuclei decreases.
Spin - spin relaxation
Spin - spin relaxation describes the interaction between neighbouring nuclei with identical precessional frequencies but differing magnetic quantum states. In this situation, the nuclei can exchange quantum states; a nucleus in the lower energy level will be excited, while the excited nucleus relaxes to the lower energy state. There is no net change in the populations of the energy states, but the average lifetime of a nucleus in the excited state will decrease. This can result in line-broadening.
The magnetic field at the nucleus is not equal to the applied magnetic field; electrons around the nucleus shield it from the applied field. The difference between the applied magnetic field and the field at the nucleus is termed the nuclear shielding.
Consider the s-electrons in a molecule. They have spherical symmetry and circulate in the applied field, producing a magnetic field which opposes the applied field. This means that the applied field strength must be increased for the nucleus to absorb at its transition frequency. This upfield shift is also termed diamagnetic shift.
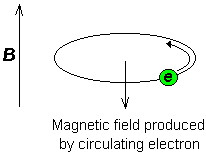
Electrons in p-orbitals have no spherical symmetry. They produce comparatively large magnetic fields at the nucleus, which give a low field shift. This "deshielding" is termed paramagnetic shift.
In proton (1H) NMR, p-orbitals play no part (there aren't any!), which is why only a small range of chemical shift (10 ppm) is observed. We can easily see the effect of s-electrons on the chemical shift by looking at substituted methanes, CH3X. As X becomes increasingly electronegative, so the electron density around the protons decreases, and they resonate at lower field strengths (increasing dH values).
Chemical shift is defined as nuclear shielding / applied magnetic field. Chemical shift is a function of the nucleus and its environment. It is measured relative to a reference compound. For 1H NMR, the reference is usually tetramethylsilane, Si (CH3)4.
Consider the structure of ethanol;
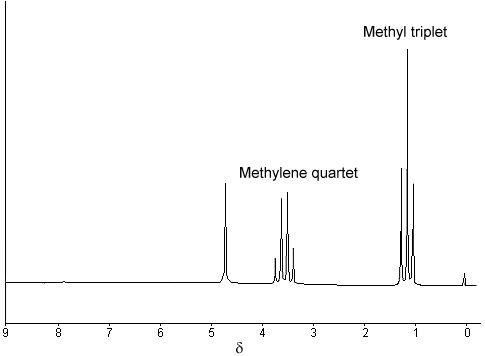
The 1H NMR spectrum of ethanol (below) shows the methyl peak has been split into three peaks (a triplet) and the methylene peak has been split into four peaks (a quartet). This occurs because there is a small interaction (coupling) between the two groups of protons. The spacings between the peaks of the methyl triplet are equal to the spacings between the peaks of the methylene quartet. This spacing is measured in Hertz and is called the coupling constant, J.
To see why the methyl peak is split into a triplet, let's look at the methylene protons. There are two of them, and each can have one of two possible orientations (aligned with or opposed against the applied field). This gives a total of four possible states;
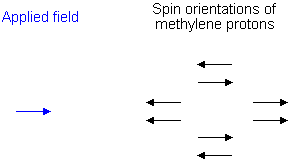
In the first possible combination, spins are paired and opposed to the field. This has the effect of reducing the field experienced by the methyl protons; therefore a slightly higher field is needed to bring them to resonance, resulting in an upfield shift. Neither combination of spins opposed to each other has an effect on the methyl peak. The spins paired in the direction of the field produce a downfield shift. Hence, the methyl peak is split into three, with the ratio of areas 1:2:1.
Similarly, the effect of the methyl protons on the methylene protons is such that there are eight possible spin combinations for the three methyl protons;
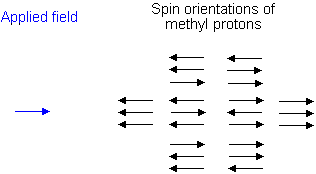
Out of these eight groups, there are two groups of three magnetically equivalent combinations. The methylene peak is split into a quartet. The areas of the peaks in the quartet have the ration 1:3:3:1.
In a first-order spectrum (where the chemical shift between interacting groups is much larger than their coupling constant), interpretation of splitting patterns is quite straightforward;
You should now be familiar with the basic principles of NMR spectroscopy, such as the splitting of nuclear energy levels in a magnetic field and how a transition between the levels can be induced. You should understand the mechanisms by which an excited nucleus can return to the lower energy level. You should also understand how the chemical environment of a nucleus gives rise to chemical shift and spin-spin splitting patterns.
|
|
|

 Biosciences Homepage
Biosciences Homepage
 |